Số thực là gì?

Số thực là gì, tập hợp số thực gồm những số nào? Mời các bạn đọc bài viết dưới đây để hiểu rõ hơn về kiến thức toán học quan trọng này nhé.

Số thực là gì?

Số thực là tập hợp bao gồm số dương (1,2,3), số 0, số âm (-1,-2,-3), số hữu tỉ (5/2, -23/45), số vô tỉ (số pi, số √ 2).

Số thực có thể được xem là các điểm nằm trên trục số dài vô hạn.

Hiểu một cách đơn giản hơn thì số thực là tập hợp các số hữu tỉ và vô tỉ.

Tập hợp số thực kí hiệu là R (R = Q U I). Trong tiếng Anh số thực là Real numbers.

Ngoài ra, một số thực có thể là số đại số hoặc số siêu việt. Ta cũng có số thực âm (-1, -3/4…) và số thực dương (5, 7, √ 2…).

Như vậy, Số tự nhiên, số nguyên, số hữu tỉ và số vô tỷ đều thuộc tập hợp số thực. Chúng lấp đầy trên trục số.

Số thực bao gồm những số nào?

Số thực gồm:

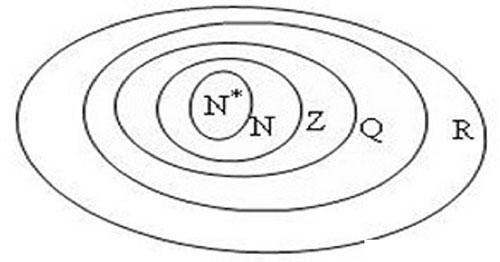
• Số tự nhiên N: N = {0, 1, 2, 3…}
• Số nguyên Z: Z = {…-3, -2, -1, 0, 1, 2, 3…}
• Số hữu tỉ Q: Q = {x = a/b; trong đó a,b ϵ Z, và b ≠0}
• Số vô tỉ I: I ={thập phân vô hạn không tuần hoàn, ví dụ căn
  bậc 2}

Trục số thực là gì?

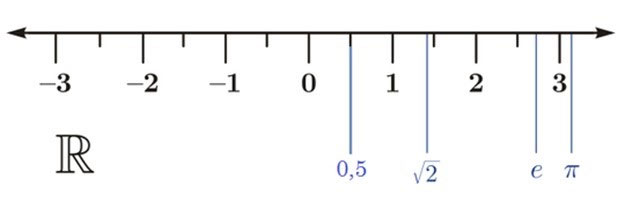
Mỗi số thực được biểu diễn bởi một điểm trên trục số.

Ngược lại mỗi điểm trên trục số đều biểu diễn một số thực.

Chỉ có tập hợp số thực mới lấp đầy trục số.

Chú ý: Các phép toán trong tập hợp các số thực cũng có các tính chất tương tự như các phép toán trong tập hợp số hữu tỉ. Ta có Z ⊂ Q ⊂ R.

Chúng ta được biết, Tập hợp số thực được đặt làm đối trọng với tập hợp số phức. Trong đó, số phức còn được gọi là số ảo, tức không thể biểu diễn trên trục số, cũng như có nhiều phương trình và bài toán không thể giải được trong trường số phức. Ví dụ như (x + 1) = -9, hay như phép tính √ -1 (căn bậc hai của -1 và các số âm khác).

Các phép toán

Trong tập hợp số thực R, ta cũng định nghĩa các phép toán cộng, trừ, nhân chia, lũy thừa và khai căn. Các phép toán trong tập hợp số thực cũng có các tính chất như các phép toán trong tập hợp các số hữu tỉ.

Trong tập hợp các số thực, các phép tính có các tính chất đối với phép nhân như sau:

Với a, b, c là các số thực ta có:

• Tính chất giao hoán: a. b = b. a;

• Tính chất kết hợp: (a. b). c = a. (b. c);

• Tính chất nhân với số 1: a. 1 = 1. a = a;

• Tính chất phân phối của phép nhân đối với phép cộng: a. (b + c) = a. b + a. c;

• Với mỗi số thực a ≠ 0, có số nghịch đảo 1a1asao cho a.1a=1a.1a=1.

Ta có thể chuyển phép chia cho một số thực khác 0 về phép nhân với số nghịch đảo của số thực đó:

a : b = a.1ba.1b(với b ≠ 0)

Công thức tính giá trị tuyệt đối của một số thực

Khái niệm: Khoảng cách từ điểm x đến điểm gốc O trên trục số được gọi là giá trị tuyệt đối của số x, kí hiệu là |x|.

• Với mọi số thực x thì |x| ≥ 0;

• Với mọi số thực x thì |‒x| = |x|;

Tính chất:

• Nếu x > 0 thì |x| = x.

• Nếu x = 0 thì |x| = 0.

• Nếu x < 0 thì |x| = ‒x.

Ta cũng có thể viết như sau:

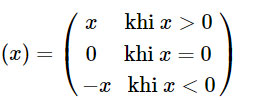
+ Với số thực không âm a ≥ 0, ta có: |x| = a thì x = a hoặc x = −a;

+ Với mọi số thực x, y ta có: |x| = |y| thì x = a hoặc x = −y.

Ví dụ: tìm |-3,14|; ;

Giải: 

|-3,14| = -(-3,14) = 3,14

Bài tập ví dụ về số thực

Ví dụ 1: Điền dấu ∈, ∉, ⊂ thích hợp vào chỗ trống (…):

3 …. Q ; 3 …. R ; 3… I ; -2,53… Q ;

0,2(35) …. I ; N …. Z ; I …. R.

Giải:

a) 3 ∈ Q ; 3 ∈ R ; 3 ∉ I ; -2,53∈ Q ;

b) 0,2(35) ∉ I ; N ∈ Z ; I ⊂ R.

Ví dụ 2: Hãy tìm các tập hợp

a) Q ∩ I ;
b) R ∩ I.

Giải.

a) Q ∩ I = Ø ;
b) R ∩ I = I.

Ví dụ 3: Điền chữ số thích hợp vào (…) 

a) – 3,02 < – 3, … 1
b) – 7,5 … 8 > – 7,513 ;
c) – 0,4 … 854 < – 0,49826 ;
d) -1, … 0765 < – 1,892.

Hướng dẫn

a) – 3,02 < – 301
b) – 7,508 > – 7,513 ;
c) – 0,49854 < – 0,49826 ;
d) -1,90765 < – 1,892.

Ví dụ 4: Tìm x, biết:

3,2.x + (-1,2).x +2,7 = -4,9;

Giải.

3,2. x + (-1,2).x + 2,7 = -4,9

[3,2 + (-1,2)].x + 2,7 = -4,9.

2.x + 2,7 = – 4,9.

2.x = – 4,9 – 2,7

2.x = – 7,6

x = -7,6 : 2

x = -3,8

Ngoài số thực, các bạn có thể tìm hiểu thêm về các định nghĩa khác trong toán học như số chính phương, số vô tỉ, số hữu tỉ, số nguyên tố, số tự nhiên...